间断有限元方法 (DG) 是连续有限元方法的创新、改进和发展, 它的检验函数和试探函数采用完全不连续的多项式. 相比于连续元, DG 方法具有很多优势, 如: 允许带有悬挂点的不相容网格剖分; hp 自适应更加灵活和高效; 离散方程组具有良好的并行计算结构等.
本文档 基于 FEALPY, 用自适应直接间断有限元方法 (DDG) 求解二阶带有间断系数的椭圆方程, 主要介绍DDG 离散格式和残量型后验误差估计子的程序实现, 并展示一个具体的数值案例, 完整的程序请参考 FEALPY/example/ADDG, 更多的理论细节请参考 [1].
1. 模型问题与 DDG 离散
1.1. PDE 模型
令 $\Omega \in \mathbb{R}^2$ 是有界多边形开区域, $\partial \Omega = \Gamma_D\cup \Gamma_N$ 且 $\Gamma_D\cap \Gamma_N = \emptyset$, $mes(\Gamma_{D})\ge 0$. 考虑如下二阶椭圆型偏微分方程:
\[\begin{aligned} -\nabla \cdot (a(x)\nabla u) = f, \qquad & \mathbf{x} \in \Omega, \\ u = g_D, \qquad & \mathbf{x} \in \Gamma_D,\\ \mathbf{n}\cdot(a(x)\nabla u)= g_N, \qquad & \mathbf{x} \in \Gamma_N. \end{aligned}\]其中, $f \in L^2(\Omega),\,g_D\in H^{\frac{1}{2}}(\Gamma_D),\,g_N\in L^2(\Gamma_N)$ 是已知函数, $\mathbf{n}=(n_1,n_2)$ 是边上的单位外法向量, 扩散系数 $a(x)$ 在 $\Omega$ 中是正的分片常数, 即
\[a(x) = a_i>0,\,\, x \in \Omega_i,\quad i =1,\cdots,n.\]其中开多边形区域 ${\Omega_i}_{i = 1}^n$ 是 $\Omega$ 的子域.
1.2. 有限元空间
令 $\mathcal{T}_h$ 是 $\Omega$ 上的三角网格剖分, 假设
(1) $\mathcal{T}_h$ 中的单元是形状正则的, 即:
\[\forall K\in \mathcal{T}_h,\,\exists c_0>0, \quad s.t \quad h_K \rho_K \le c_0.\]其中 $h_K,\,\rho_K$ 分别是单元 $K$ 的网格尺寸和内接圆直径.
(2) $\mathcal{T}_h$ 是局部拟一致的, 即:
\[\text{如果} \quad \partial \overline{K_i} \cap \partial \overline{K_j} \ne \varnothing, \,\,\text{则} \quad h_{K_i}\approx h_{K_j}.\](3) 网格 $\mathcal{T}_h$ 是匹配的, 即: 界面 $I = {\partial \Omega_i \cap \partial \Omega_j:\,i,j = 1,2,\cdots n}$ 不出穿过 $\mathcal{T}_h$ 中任意单元 $K$.
在剖分 \(\mathcal{T}_h\) 上定义间断有限元空间 $V_{DG}^{p}$ :
\[\begin{aligned} V_{DG}^{\ell} = \{v\in L^2(\Omega):v|_K\in \mathbb{P}_{\ell}(K),\, \forall \,K\in \mathcal{T}_h\}. \end{aligned}\]1.3. 跳量和均值
令 $\mathcal{T}_h$ 上边的集合为 $\mathcal{E}$, $K \in \mathcal{T}_h$ 上边的集合为 $\mathcal{E}_K$, 对 $e \in \mathcal{E}$, $h_e$ 为其边长. 定义 $\Omega,\,\Gamma_D,\,\Gamma_N$ 上边的集合分别为:
\[\begin{aligned} \mathcal{E}_{I}&=\{e \in \mathcal{E} : e \subset \Omega\}, \\ \mathcal{E}_{D}&=\left\{e \in \mathcal{E} : e \subset \Gamma_{D}\right\}, \\ \mathcal{E}_{N}&=\left\{e \in \mathcal{E} : e \subset \Gamma_{N}\right\}. \end{aligned}\]为了方便, 记
\[\mathcal{E}_{ID}=\mathcal{E}_{I} \cup \mathcal{E}_{D},\,\mathcal{E}_{B}=\mathcal{E}_{D} \cup \mathcal{E}_{N}.\]当 \(e \in \mathcal{E}_{I}\), 记 $K_+,\,K_-$ 为 $e$ 的左右单元, 其中 $K_+$ 是整体单元编号较大的单元, $\mathbf{n}$ 为 $e$ 由 $K_+$ 指向 $K_-$ 的单位外法向量. 当 \(e \in \mathcal{E}_{B}\), $K_+$ 是 $e$ 上的单元, $\mathbf{n}$ 是 $e$ 的单位外法向量.
对 $v \in V_{DG}^{\ell}$, 跳量的定义为:
\[[v] := \begin{cases} v_+ - v_-,\quad &e \in \mathcal{E}_{I}, \\ v_+,\quad &e \in \mathcal{E}_{B}. \end{cases}\]均值的定义为:
\[\begin{aligned} \{v\}_w := \begin{cases} w_+v_+ + w_-v_-,\quad &e \in \mathcal{E}_{I}, \\ v_+,\quad &e \in \mathcal{E}_{B}, \end{cases}\qquad\qquad\qquad\qquad \{v\}^w := \begin{cases} w_-v_+ + w_+v_-,\quad &e \in \mathcal{E}_I, \\ 0,\quad &e \in \mathcal{E}_B, \end{cases} \end{aligned}\]其中权重 $w_+,\,w_- \in [0,1]$, 满足: $w_+ + w_- = 1$.
对任意 \(e \in \mathcal{E}_{I},\,e = \partial K_+ \cap \partial K_-\) , 令 $a_+,\,a_-$ 分别是 $K_+,\,K_+$ 上的扩散系数, 定义 $a$ 在 $e$ 上的加权平均为
\[W_{e,i} = w_{+,i}\,a_+ + w_{-,i}\,a_-,\quad i = 1,2,3.\]\(W_{e,i}\) 分别为算数、调和、几何平均
\[W_{e,1} = \frac{a_+ + a_-}{2},\quad W_{e,2} = \frac{2a_+ a_-}{a_+ + a_-},\quad W_{e,3} = \sqrt{a_+ a_-},\]对任意 \(e \in \mathcal{E}_{B},\,e = \partial K_+\cap\partial \Omega\), $a$ 在 $e$ 上的加权平均为
\[W_{e,i} = a_+ .\]为了叙述方便, 以下我们选 \(W_e = \{a\}_w = W_{e,2}\).
1.4. DDG 离散格式
定义数值通量:
\[\widehat{a u_\mathbf{n}}|_e = \begin{cases} -\beta_1 h_e^{-1}W_e\,[u] + \{a\,u_\mathbf{n}\}_w - \beta_2h_eW_e\,[u_{\mathbf{n}\mathbf{n}}],\quad e \in \mathcal{E}_{I},\\ -\beta_1 h_e^{-1}W_e\,(u-g_D) + a\,u_\mathbf{n}, \qquad \qquad\qquad e \in \mathcal{E}_{D},\\ g_N, \qquad \qquad\qquad\qquad \qquad\qquad\qquad e \in \mathcal{E}_{N}, \end{cases}\] \[\widehat {u}|_e = \begin{cases} \{u\}^w,\qquad& e \in \mathcal{E}_{I},\\ g_D,\qquad& e \in \mathcal{E}_{D},\\ u,\qquad& e \in \mathcal{E}_{N}. \end{cases}\]记单元 $K$ 和 边 $e$ 上的 $L^2$ 内积分别为 $(\cdot,\cdot)_K,\,\langle \cdot,\cdot \rangle_e$. 定义 双线性型 $a_h(\cdot,\cdot)$ 和 线性型 $f_h(\cdot)$ 如下:
\[\begin{aligned} a_h(u,v) &= \sum_{K \in \mathcal{T}_h}(a\nabla u,\nabla v)_K + \sum_{e \in \mathcal{E}_{ID}}\Big[\beta_1 h_e^{-1}W_e \langle [u],[v]\rangle_e-\langle \{a\,u_\mathbf{n}\}_w,[v]\rangle_e - \langle \{a\,v_\mathbf{n}\}_w,[u]\rangle_e\Big] \\ &+ \sum_{e \in \mathcal{E}_{I} }\beta_2h_eW_e\langle[u_{\mathbf{n}\mathbf{n}}],[v]\rangle_e,\\ f_h(v) &= \sum_{K \in \mathcal{T}_h}(f,v)_K + \sum_{e \in \mathcal{E}_{N}}\langle g_N,v\rangle_e- \sum_{e \in \mathcal{E}_{D}} \langle g_D,a\,v_\mathbf{n}\rangle_e + \beta_1 h_e^{-1}W_e\sum_{e \in \mathcal{E}_{D}} \langle g_D,v\rangle_e . \end{aligned}\]则模型问题相应的 DDG 离散格式为: 求 $u_h\in V_{DG}^{\ell}$, 使得
\[a_h(u_h,v_h) = f_h(v_h) ,\quad \forall v_h \in V_{DG}^{\ell}.\]1.5. DDG 离散格式程序实现
1.5.1. 计算单元刚度矩阵 \((a \nabla u_h,\nabla v_h)_K = \int_{K}a \nabla u_h \cdot \nabla v_h\, \mathrm{dxdy}\)
记 $n$ 为单元上自由度个数, $N$ 为全局自由度, $NC$ 为剖分 \(\mathcal{T}_h\) 上的单元个数, \(\{p_j\}_{j=0}^{t_c-1}\) 为每个单元上取的高斯点, \(\{q_j\}_{j=0}^{t_e-1}\) 为每条边上取的高斯点. 对任意的单元 \(K \in \mathcal{T}_h\), 令
\[\begin{aligned} \Phi_{K} = \begin{bmatrix} \phi_0 & \phi_1 & \cdots & \phi_{n-1} \end{bmatrix}_{1\times n},\qquad U_{K} = \begin{bmatrix} u_0\\ \vdots\\ u_{n-1} \end{bmatrix}_{n\times 1} \end{aligned}\]则有
\[\begin{aligned} u_h|_K = \sum_{j =0}^{n-1}u_j\phi_j = \Phi_{K}U_{K} \end{aligned}\]故
\[\begin{aligned} \nabla u_h|_{K} = \begin{bmatrix} \nabla\phi_0 & \nabla\phi_1 & \cdots & \nabla\phi_{n-1} \end{bmatrix} \begin{bmatrix} u_0\\ \vdots\\ u_{n-1} \end{bmatrix} = \nabla\Phi_{K}U_{K} \end{aligned}\]其中
\[\begin{aligned} \nabla\Phi_{K}= \begin{bmatrix} \nabla \phi_0 & \nabla\phi_1 & \cdots & \nabla\phi_{n-1} \end{bmatrix} \end{aligned}\]同理有: \(\begin{aligned} v_h|_{K} = \Phi_{K}V_{K}, \qquad \nabla v_h|_{K} = \nabla\Phi_{K}V_{K} \end{aligned}\)
故
\[\begin{align*} (a\nabla u_h,\nabla v_h)_{K} &= \int_{K} a\nabla u_h \cdot \nabla v_h\, \mathrm{dxdy}\\ &= V_{K}^T\int_{K}a\nabla \Phi_{K}^T\nabla\Phi_{K}\, \mathrm{dxdy}U_{K} \\ & = V_{K}^TA_{K}U_{K}, \end{align*}\]其中
\[\begin{align*} A_{K} = \int_{K}a\nabla\Phi_{K}^T\nabla\Phi_{K}\, \mathrm{dxdy} &= \begin{bmatrix} a\nabla \phi_0^T \\ a\nabla \phi_1^T\\ \vdots \\ a\nabla \phi_{n-1}^T \end{bmatrix} \begin{bmatrix} \nabla \phi_0^T & \nabla \phi_1^T & \cdots & \nabla \phi_{n-1}^T \end{bmatrix}\\ &=\begin{bmatrix} (a\nabla\phi_0,\nabla\phi_0)_{K} &(a\nabla\phi_0,\nabla\phi_1)_{K} & \cdots &(a\nabla\phi_0,\nabla\phi_{n-1})_{K}\\ (a\nabla\phi_1,\nabla\phi_0)_{K} &(a\nabla\phi_1,\nabla\phi_1)_{K} & \cdots &(a\nabla\phi_1,\nabla\phi_{n-1})_{K}\\ \vdots & \vdots & \vdots & \vdots \\ (a\nabla\phi_{n-1},\nabla\phi_0)_{K} &(a\nabla\phi_{n-1},\nabla\phi_1)_{K} & \cdots &(a\nabla\phi_{n-1},\nabla\phi_{n-1})_{K} \end{bmatrix}_{n\times n} \end{align*}\]程序实现:
def DDG_stiff_matrix(self,qf, cfun=None):
bcs =qf.quadpts
ws = qf.weights
mesh = self.mesh
GD = mesh.node.shape[1]
NC = mesh.number_of_cells()
pp = self.bc_to_point_cell(bcs)
cellidx = np.arange(NC)
ldof = self.number_of_local_dofs()
gdof = self.number_of_global_dofs()
G_Basis = self.Hat_Gradients(pp,cellidx)
if cfun is not None:
d = cfun(pp)
dG_Basis = np.einsum('i, ...imn->...imn', d, G_Basis)
else:
dG_Basis = G_Basis
A = np.einsum('t, tmkj, tmpj,m->mkp', ws, dG_Basis, G_Basis, self.cellmeasure)
cell2dof = self.cell_to_dof()
I = np.einsum('k, ij->ijk', np.ones(ldof), cell2dof)
J = I.swapaxes(-1, -2)
A = csr_matrix((A.flat, (I.flat, J.flat)), shape=(gdof, gdof))
return A
1.5.2. 计算边矩阵 $P_e= \beta_1 h_e^{-1}W_e \langle [u],[v]\rangle_e$,
当 $e_i \in \mathcal{E}_{I},\,e = \partial K^+ \cap \partial K^-$ 时, 由跳量的定义 $[u] = u^+ - u^-$ 知, 令
\[\begin{align} Jump = [\Phi_{e_i}] = \begin{bmatrix} \Phi_{K^+} & -\Phi_{K^-} \end{bmatrix} = \begin{bmatrix} \phi_0^+ & \phi_1^+ & \cdots& \phi_{n-1}^+ & -\phi_0^- & -\phi_1^- & \cdots& \phi_{n-1}^- \end{bmatrix}_{1\times 2n}. \end{align}\]当 \(e_i \in \mathcal{E}_{D},\,e = \partial K_+ \cap \partial \Omega\) 时, 取 \(\phi_0^- = \cdots = \phi_{n-1}^- =0\), 即:
\[\begin{align} Jump = \begin{bmatrix} \phi_0^+ &\phi_1^+ &\cdots&\phi_n^+ & 0 & 0 &\cdots & 0 \end{bmatrix}_{1\times 2n}.\label{jump2} \end{align}\]令
\[\begin{align} U_{e_i} = \begin{bmatrix} u_0^+\\ \vdots\\ u_n^+\\ u_0^-\\ \vdots\\ u_{n-1}^- \end{bmatrix}_{2n\times 1},\quad V_{e_i} = \begin{bmatrix} v_0^+\\ \vdots\\ v_{n-1}^+\\ v_0^-\\ \vdots\\ v_{n-1}^- \end{bmatrix}_{2n\times 1} \end{align}\]由基函数跳量的定义, 当 $e_i \in \mathcal{E}$时, 有
\[\begin{align} [u_h]|_{e_i} = u_e^+ -u_e^- = \sum_{i = 0}^{n-1}\phi_i^+ {u_i}^ + - \sum_{i = 0}^{n-1}\phi_i^- {u_i}^ - = [\Phi_{e_i}]U_{e_i}\\ [v_h]|_{e_i} = v_e^+ -v_e^- =\sum_{i = 0}^{n-1}\phi_i^+ {v_i}^ + - \sum_{i = 0}^{n-1}\phi_i^- {v_i}^ - = [\Phi_{e_i}]V_{e_i} \end{align}\]故
\[h_{e_i}^{-1}\langle [u_h],[v_h]\rangle_{e_i} = h_e^{-1}\int_{e_i}V_{e_i}^T[\Phi_{e_i}]^T[\Phi_{e_i}]U_{e_i}\,\mathrm{ds} = V_{e_i}^Th_e^{-1}\int_{e_i} [\Phi_{e_i}]^T[\Phi_{e_i}]\,\mathrm{ds}\,U_{e_i} = V_{e_i}^T P_{e_i} U_{e_i}\]其中 $P_{e_i}$ 是规模为 $2n\times 2n$ 的单边上的惩罚矩阵, 即
\[\begin{align*} P_{e_i} = h_e^{-1}\int_{e_i}[\Phi_{e_i}]^T[\Phi_{e_i}]\,\mathrm{s}&= h_{e_i}^{-1}\cdot \begin{bmatrix} \phi_0^+\\ \vdots\\ \phi_{n-1}^+\\ \phi_0^-\\ \vdots\\ \phi_{n-1}^- \end{bmatrix} \begin{bmatrix} \phi_0^+ & \cdots &\phi_{n-1}^+ &\phi_0^- &\cdots &\phi_{n-1}^- \end{bmatrix}_{2n\times 2n}\\ &= h_{e_i}^{-1}\cdot\begin{bmatrix} \langle \phi_0^+,\phi_0^+ \rangle_{e_i} & \langle \phi_0^+,\phi_1^+ \rangle_{e_i} &\cdots& \langle \phi_0^+,\phi_{n-1}^+ \rangle_{e_i} & \langle \phi_0^+,-\phi_0^- \rangle_{e_i} & \langle \phi_0^+,-\phi_1^- \rangle_{e_i} &\cdots& \langle \phi_0^+,-\phi_{n-1}^- \rangle_{e_i}\\ \langle \phi_1^+,\phi_0^+ \rangle_{e_i} & \langle \phi_1^+,\phi_1^+ \rangle_{e_i} &\cdots & \langle \phi_1^+,\phi_{n-1}^+ \rangle_{e_i} & \langle \phi_1^+,-\phi_0^- \rangle_{e_i} & \langle \phi_1^+,-\phi_1^- \rangle_{e_i} &\cdots& \langle \phi_1^+,-\phi_{n-1}^- \rangle_{e_i}\\ \vdots & \vdots & \vdots &\vdots &\vdots &\vdots &\vdots &\vdots\\ \langle \phi_{n-1}^+,\phi_0^+ \rangle_{e_i} & \langle \phi_{n-1}^+,\phi_1^+ \rangle_{e_i} &\cdots& \langle \phi_{n-1}^+,\phi_{n-1}^+ \rangle_{e_i} & \langle \phi_{n-1}^+,-\phi_0^- \rangle_{e_i} & \langle \phi_{n-1}^+,-\phi_1^- \rangle_{e_i} &\cdots& \langle \phi_{n-1}^+,-\phi_{n-1}^- \rangle_{e_i}\\ \langle -\phi_0^-,\phi_0^+ \rangle_{e_i} & \langle -\phi_0^-,\phi_1^+ \rangle_{e_i} &\cdots& \langle -\phi_0^-,\phi_{n-1}^+ \rangle_{e_i} & \langle -\phi_0^-,-\phi_0^- \rangle_{e_i} & \langle -\phi_0^-,-\phi_1^- \rangle_{e_i} &\cdots& \langle -\phi_0^-,-\phi_{n-1}^- \rangle_{e_i}\\ \langle -\phi_1^-,\phi_0^+ \rangle_{e_i} & \langle -\phi_1^-,\phi_1^+ \rangle_{e_i} &\cdots& \langle -\phi_1^-,\phi_{n-1}^+ \rangle_{e_i} & \langle -\phi_1^-,-\phi_0^- \rangle_{e_i} & \langle -\phi_1^-,-\phi_1^- \rangle_{e_i} &\cdots& \langle -\phi_1^-,-\phi_{n-1}^- \rangle_{e_i}\\ \vdots & \vdots & \vdots &\vdots &\vdots &\vdots &\vdots &\vdots\\ \langle -\phi_{n-1}^-,\phi_0^+ \rangle_{e_i} & \langle -\phi_{n-1}^-,\phi_1^+ \rangle_{e_i} &\cdots& \langle -\phi_{n-1}^-,\phi_{n-1}^+ \rangle_{e_i} & \langle -\phi_{n-1}^-,-\phi_0^- \rangle_{e_i} & \langle -\phi_{n-1}^-,-\phi_1^- \rangle_{e_i}&\cdots & \langle -\phi_{n-1}^-,-\phi_{n-1}^- \rangle_{e_i} \end{bmatrix}_{2n\times 2n}. \end{align*}\]当 $e \in \mathcal{E}_D$ 时,
\[\begin{align} P_{e_i} = h_{e_i}^{-1}\cdot\begin{bmatrix} \langle \phi_0^+,\phi_0^+ \rangle_{e_i} & \langle \phi_0^+,\phi_1^+ \rangle_{e_i} &\cdots& \langle \phi_0^+,\phi_{n-1}^+ \rangle_{e_i} &0 & 0 &\cdots& 0\\ \langle \phi_1^+,\phi_0^+ \rangle_{e_i} & \langle \phi_1^+,\phi_1^+ \rangle_{e_i} &\cdots & \langle \phi_1^+,\phi_{n-1}^+ \rangle_{e_i} &0 & 0&\cdots& 0\\ \vdots & \vdots & \vdots &\vdots &\vdots &\vdots &\vdots &\vdots\\ \langle \phi_{n-1}^+,\phi_0^+ \rangle_{e_i} & \langle \phi_{n-1}^+,\phi_1^+ \rangle_{e_i} &\cdots& \langle \phi_{n-1}^+,\phi_{n-1}^+ \rangle_{e_i} &0& 0 &\cdots&0\\ 0 &0 &\cdots&0 &0& 0&\cdots& 0\\ 0 & 0 &\cdots& 0 &0& 0 &\cdots& 0\\ \vdots & \vdots & \vdots &\vdots &\vdots &\vdots &\vdots &\vdots\\ 0& 0 &\cdots& 0 &0 &0&\cdots & 0 \end{bmatrix}_{2n\times 2n}. \end{align}\]1.5.3. 计算边矩阵 $ S_e = \langle {a\,u_\mathbf{n}}_w,[v]\rangle_e$
当 $e_i \in \mathcal{E}_{I},\,e = \partial K^+ \cap \partial K^-$ 上, 由均值的定义 ${u} = \frac{1}{2}(u^+ + u^-)$ 知,
\[\begin{align} Average = \{a\nabla\Phi_{e_i}\}&= \frac{1}{2} \begin{bmatrix}(a\nabla \Phi)_{K^+} & (a\nabla \Phi)_{K^-} \end{bmatrix} \\ &=\begin{bmatrix} \frac{1}{2}a^+\nabla\phi_0^+ & \frac{1}{2}a^+\nabla\phi_1^+ & \cdots &\frac{1}{2}a^+\nabla\phi_{n-1}^+ &\frac{1}{2}a^-\nabla\phi_0^- & \frac{1}{2}a^-\nabla\phi_1^- & \cdots & \frac{1}{2}a^-\nabla\phi_{n-1}^- \end{bmatrix}_{2 \times 2n}. \end{align}\]当 \(e_i \in \mathcal{E}_{D},\,e = \partial K^+ \cap \partial \Omega\) 时, 取 \(\nabla \phi_0^- = \cdots = \nabla\phi_{n-1}^- = 0\), 令
\[\begin{align} Average = \begin{bmatrix} a^+\nabla\phi_0^+ & a^+\nabla\phi_1^+ &\cdots& a^+\nabla\phi_n^+ &0 & 0 &\cdots& 0 \end{bmatrix}_{2 \times 2n}. \end{align}\]令 \(\mathbf{n} = [\mathbf{n}_x,\mathbf{n}_y]_{1\times 2}\), 由基函数均值的定义的定义知
\[\begin{align} \{a \nabla u_h\cdot\mathbf{n}\} = \mathbf{n}\cdot\{a\nabla\Phi_{e_i}\}U_{e_i} \end{align}\]故
\[\begin{align} \langle \{a\nabla u_h\cdot\mathbf{n}\},[v_h]\rangle_{e_i} = \int_{e_i}V_{e_i}^T[\Phi_{e_i}]^T\mathbf{n}\cdot\{a\nabla\Phi_{e_i}\}U_{e_i}\,\mathrm{ds} = V_{e_i}^T\int_{e_i}[\Phi_{e_i}]^T\mathbf{n}\cdot \{a\nabla\Phi_{e_i}\}\,\mathrm{ds}U_{e_i} = V_{e_i}^TS_{e_i}U_{e_i}, \end{align}\]其中 $S_{e_i}$ 是规模为 $2n\times2n$ 的单边流通矩阵.
当 $e_i \in \mathcal{E}_{I},\,e = \partial K^+ \cap \partial K^-$ 上:
\[\begin{align} S_{e_i} & = \int_{e_i}[\Phi_{e_i}]^T\mathbf{n}\cdot \{a\nabla\Phi_{e_i}\}\,\mathrm{ds} = \begin{bmatrix} \phi_0^+\\ \vdots\\ \phi_{n-1}^+\\ \phi_0^-\\ \vdots\\ \phi_{n-1}^- \end{bmatrix} \begin{bmatrix} a^+\nabla\phi_0^+ & \cdots & a^+\nabla \phi_{n-1}^+ &a^- \nabla \phi_0^- & \cdots &a^-\nabla \phi_{n-1}^- \end{bmatrix} \\ &= \frac{1}{2}\cdot\begin{bmatrix} \langle \phi_0^+,\mathbf{n}\cdot a^+\nabla\phi_0^+ \rangle_{e_i} & \langle \phi_0^+,\mathbf{n}\cdot a^+\nabla\phi_1^+ \rangle_{e_i} & \cdots& \langle \phi_0^+,\mathbf{n}\cdot a^+\nabla\phi_{n-1}^+ \rangle_{e_i} & \langle \phi_0^+,\mathbf{n}\cdot a^-\nabla\phi_0^- \rangle_{e_i} & \langle \phi_0^+,\mathbf{n}\cdot a^-\nabla\phi_1^- \rangle_{e_i} & \cdots& \langle \phi_0^+,\mathbf{n}\cdot a^-\nabla\phi_{n-1}^- \rangle_{e_i}\\ \langle \phi_1^+,\mathbf{n}\cdot a^+\nabla\phi_0^+ \rangle_{e_i} & \langle \phi_1^+,\mathbf{n}\cdot a^+\nabla\phi_1^+ \rangle_{e_i} & \cdots& \langle \phi_1^+,\mathbf{n}\cdot a^+\nabla\phi_{n-1}^+ \rangle_{e_i} & \langle \phi_1^+,\mathbf{n}\cdot a^-\nabla\phi_0^- \rangle_{e_i} & \langle \phi_1^+,\mathbf{n}\cdot a^-\nabla\phi_1^- \rangle_{e_i} & \cdots& \langle \phi_1^+,\mathbf{n}\cdot a^-\nabla\phi_{n-1}^- \rangle_{e_i}\\ \vdots& \vdots& \cdots& \vdots& \vdots& \vdots& \cdots& \vdots&\\ \langle \phi_{n-1}^+,\mathbf{n}\cdot a^+\nabla\phi_0^+ \rangle_{e_i} & \langle \phi_{n-1}^+,\mathbf{n}\cdot a^+\nabla\phi_1^+ \rangle_{e_i} & \cdots& \langle \phi_{n-1}^+,\mathbf{n}\cdot a^+\nabla\phi_{n-1}^+ \rangle_{e_i} & \langle \phi_{n-1}^+,\mathbf{n}\cdot a^-\nabla\phi_0^- \rangle_{e_i} & \langle \phi_{n-1}^+,\mathbf{n}\cdot a^-\nabla\phi_1^- \rangle_{e_i} & \cdots& \langle \phi_{n-1}^+,\mathbf{n}\cdot a^-\nabla\phi_{n-1}^- \rangle_{e_i}\\ \langle -\phi_0^-,\mathbf{n}\cdot a^+\nabla\phi_0^+ \rangle_{e_i} & \langle -\phi_0^-,\mathbf{n}\cdot a^+\nabla\phi_1^+ \rangle_{e_i} & \cdots& \langle -\phi_0^-,\mathbf{n}\cdot a^+\nabla\phi_{n-1}^+ \rangle_{e_i} & \langle -\phi_0^-,\mathbf{n}\cdot a^-\nabla\phi_0^- \rangle_{e_i} & \langle -\phi_0^-,\mathbf{n}\cdot a^-\nabla\phi_1^- \rangle_{e_i} & \cdots& \langle -\phi_0^-,\mathbf{n}\cdot a^-\nabla\phi_{n-1}^- \rangle_{e_i}\\ \langle -\phi_1^-,\mathbf{n}\cdot a^+\nabla\phi_0^+ \rangle_{e_i} & \langle -\phi_1^-,\mathbf{n}\cdot a^+\nabla\phi_1^+ \rangle_{e_i} & \cdots& \langle -\phi_1^-,\mathbf{n}\cdot a^+\nabla\phi_{n-1}^+ \rangle_{e_i} & \langle -\phi_1^-,\mathbf{n}\cdot a^-\nabla\phi_0^- \rangle_{e_i} & \langle -\phi_1^-,\mathbf{n}\cdot a^-\nabla\phi_1^- \rangle_{e_i} & \cdots& \langle -\phi_1^-,\mathbf{n}\cdot a^-\nabla\phi_{n-1}^- \rangle_{e_i}\\ \vdots& \vdots& \cdots& \vdots& \vdots& \vdots& \cdots& \vdots&\\ \langle -\phi_{n-1}^-,\mathbf{n}\cdot a^+\nabla\phi_0^+ \rangle_{e_i} & \langle -\phi_{n-1}^-,\mathbf{n}\cdot a^+\nabla\phi_1^+ \rangle_{e_i} & \cdots& \langle -\phi_{n-1}^-,\mathbf{n}\cdot a^+\nabla \phi_{n-1}^+ \rangle_{e_i} & \langle -\phi_{n-1}^-,\mathbf{n}\cdot a^-\nabla\phi_0^- \rangle_{e_i} & \langle -\phi_{n-1}^-,\mathbf{n}\cdot a^-\nabla\phi_1^- \rangle_{e_i}& \cdots& \langle -\phi_{n-1}^-,\mathbf{n}\cdot a^-\nabla\phi_{n-1}^- \rangle_{e_i} \end{bmatrix}_{2n\times 2n} \end{align}\]当 $e_i \in \mathcal{E}_{D}$ 时, 有
\[\begin{align} S_{e_i} = \begin{bmatrix} \langle \phi_0^+,\mathbf{n}\cdot a^+ \nabla\phi_0^+ \rangle_{e_i} & \langle \phi_0^+,\mathbf{n}\cdot a^+\nabla\phi_1^+ \rangle_{e_i} & \cdots &\langle \phi_0^+,\mathbf{n}\cdot a^+\nabla\phi_{n-1}^+ \rangle_{e_i} &0 & 0& \cdots & 0\\ \langle \phi_1^+,\mathbf{n}\cdot a^+\nabla\phi_0^+ \rangle_{e_i} & \langle \phi_1^+,\mathbf{n}\cdot a^+\nabla\phi_1^+ \rangle_{e_i} &\cdots & \langle \phi_1^+,\mathbf{n}\cdot a^+\nabla\phi_{n-1}^+ \rangle_{e_i} &0 & 0& \cdots & 0\\ \vdots& \vdots&\cdots &\vdots&\vdots &\vdots&\cdots&\vdots\\ \langle \phi_{n-1}^+,\mathbf{n}\cdot a^+\nabla\phi_0^+ \rangle_{e_i} & \langle \phi_{n-1}^+,\mathbf{n}\cdot a^+\nabla\phi_1^+ \rangle_{e_i} & \cdots &\langle \phi_{n-1}^+,\mathbf{n}\cdot a^+\nabla\phi_{n-1}^+ \rangle_{e_i} &0 & 0& \cdots & 0\\ 0 & 0 & \cdots&0 &0 & 0& \cdots & 0\\ 0 & 0 & \cdots&0 &0 & 0 & \cdots & 0\\ \vdots& \vdots&\cdots &\vdots&\vdots &\vdots&\cdots&\vdots\\ 0 & 0 & \cdots&0 &0 & 0& \cdots & 0 \end{bmatrix}_{2n \times 2n} \end{align}\]1.5.4. 计算边矩阵 $H_e = \beta_2h_eW_e\langle[u_{\mathbf{n}\mathbf{n}}],[v]\rangle_e $.
当 $e_i \in \mathcal{E}_{I},\,e = \partial K^+ \cap \partial K^-$ 上:
\[\begin{align} [\partial_{xx}\Phi_{e_i}]&= \begin{bmatrix} \partial_{xx} \Phi_{K^+} & \partial_{xx} \Phi_{K^-} \end{bmatrix} \\ &=\begin{bmatrix} \partial_{xx}\phi_0^+ & \partial_{xx}\phi_1^+ & \cdots &\partial_{xx}\phi_{n-1}^+ &-\partial_{xx}\phi_0^- &-\partial_{xx}\phi_1^- & \cdots & -\partial_{xx}\phi_{n-1}^- \end{bmatrix}. \end{align}\] \[\begin{align} [\partial_{xy}\Phi_{e_i}]&= \begin{bmatrix} \partial_{xy} \Phi_{K^+} & \partial_{xy} \Phi_{K^-} \end{bmatrix} \\ &= \begin{bmatrix} \partial_{xy}\phi_0^+ & \partial_{xy}\phi_1^+ & \cdots &\partial_{xy}\phi_{n-1}^+ &-\partial_{xy}\phi_0^- & -\partial_{xy}\phi_1^- & \cdots &-\partial_{xy}\phi_{n-1}^-\end{bmatrix}. \end{align}\] \[\begin{align} [\partial_{yy}\Phi_{e_i}]&= \begin{bmatrix} \partial_{yy} \Phi_{K^+} & \partial_{yy} \Phi_{K^-} \end{bmatrix} \\ &=\begin{bmatrix} \partial_{yy}\phi_0^+ &\partial_{yy}\phi_1^+ & \cdots &\partial_{yy}\phi_{n-1}^+ &-\partial_{yy}\phi_0^- &- \partial\partial_{yy}\phi_1^- & \cdots & - \partial_{yy}\phi_{n-1}^- \end{bmatrix}. \end{align}\]令
\[\begin{align} [\Phi_{\mathbf{n}\mathbf{n}}]_{e_i}&= n_x^2[\partial_{xx} \Phi_{e_i}] + 2n_xn_y[\partial_{xy} \Phi_{e_i}] +n_y^2[\partial_{yy} \Phi_{e_i}]\\ & = \begin{bmatrix} (\phi_{\mathbf{n}\mathbf{n}})_0^+ &(\phi_{\mathbf{n}\mathbf{n}})_1^+ &\cdots &(\phi_{\mathbf{n}\mathbf{n}})_{n-1}^+ &-(\phi_{\mathbf{n}\mathbf{n}})_0^- &-(\phi_{\mathbf{n}\mathbf{n}})_1^- &\cdots &-(\phi_{\mathbf{n}\mathbf{n}})_{n-1}^- \end{bmatrix} \end{align}\]故
\[\begin{align} [u_{\mathbf{n}\mathbf{n}}] = [\Phi_{\mathbf{n}\mathbf{n}}]_{e_i}U_{e_i} \end{align}\]所以
\[\begin{align} h_eW_e\langle[u_{\mathbf{n}\mathbf{n}}],[v]\rangle_{e_i} = \int_{e_i}V_{e_i}^T[\Phi_{\mathbf{n}\mathbf{n}}]_{e_i}^T[\Phi_{e_i}]U_{e_i}\,\mathrm{ds} = V_{e_i}^Th_eW_e\int_{e_i}[\Phi_{\mathbf{n}\mathbf{n}}]_{e_i}^T[\Phi_{e_i}]\,\mathrm{ds}U_{e_i} = V_{e_i}^TH_{e_i}U_{e_i}, \end{align}\]其中 $H_{e_i}$ 是规模为 $2n\times2n$ 的单边矩阵.
当 $e_i \in \mathcal{E}_{I},\,e = \partial K^+ \cap \partial K^-$ 上:
\[\begin{align} H_{e_i} &= h_eW_e\int_{e_i}[\Phi_{\mathbf{n}\mathbf{n}}]_{e_i}^T[\Phi_{e_i}]\,\mathrm{ds}U_{e_i}\\ &=h_eW_e \begin{bmatrix} (\phi_{nn})_0^+\\ \vdots\\ (\phi_{nn})_{n-1}^+\\ (\phi_{nn})_0^-\\ \vdots\\ (\phi_{nn})_{n-1}^- \end{bmatrix} \begin{bmatrix} \phi_0^+ & \cdots & \phi_{n-1}^+ &\phi_0^- &\cdots &\phi_{n-1}^- \end{bmatrix}\\ =&h_eW_e\begin{bmatrix} \langle (\phi_{\mathbf{n}\mathbf{n}})_0^+,(\phi_{\mathbf{n}\mathbf{n}})_0^+ \rangle_{e_i} & \langle (\phi_{\mathbf{n}\mathbf{n}})_0^+,\phi_1^+ \rangle_{e_i} &\cdots& \langle (\phi_{\mathbf{n}\mathbf{n}})_0^+,\phi_{n-1}^+ \rangle_{e_i} & \langle (\phi_{\mathbf{n}\mathbf{n}})_0^+,-\phi_0^- \rangle_{e_i} & \langle (\phi_{\mathbf{n}\mathbf{n}})_0^+,-\phi_1^- \rangle_{e_i} &\cdots& \langle (\phi_{\mathbf{n}\mathbf{n}})_0^+,-\phi_{n-1}^- \rangle_{e_i}\\ \langle (\phi_{\mathbf{n}\mathbf{n}})_1^+,\phi_0^+ \rangle_{e_i} & \langle (\phi_{\mathbf{n}\mathbf{n}})_1^+,\phi_1^+ \rangle_{e_i} &\cdots & \langle (\phi_{\mathbf{n}\mathbf{n}})_1^+,\phi_{n-1}^+ \rangle_{e_i} & \langle (\phi_{\mathbf{n}\mathbf{n}})_1^+,-\phi_0^- \rangle_{e_i} & \langle (\phi_{\mathbf{n}\mathbf{n}})_1^+,-\phi_1^- \rangle_{e_i} &\cdots& \langle (\phi_{\mathbf{n}\mathbf{n}})_1^+,-\phi_{n-1}^- \rangle_{e_i}\\ \vdots & \vdots & \vdots &\vdots &\vdots &\vdots &\vdots &\vdots\\ \langle (\phi_{\mathbf{n}\mathbf{n}})_{n-1}^+,\phi_0^+ \rangle_{e_i} & \langle (\phi_{\mathbf{n}\mathbf{n}})_{n-1}^+,\phi_1^+ \rangle_{e_i} &\cdots& \langle (\phi_{\mathbf{n}\mathbf{n}})_{n-1}^+,\phi_{n-1}^+ \rangle_{e_i} & \langle (\phi_{\mathbf{n}\mathbf{n}})_{n-1}^+,-\phi_0^- \rangle_{e_i} & \langle (\phi_{\mathbf{n}\mathbf{n}})_{n-1}^+,-\phi_1^- \rangle_{e_i} &\cdots& \langle (\phi_{\mathbf{n}\mathbf{n}})_{n-1}^+,-\phi_{n-1}^- \rangle_{e_i}\\ \langle -(\phi_{\mathbf{n}\mathbf{n}})_0^-,\phi_0^+ \rangle_{e_i} & \langle -(\phi_{\mathbf{n}\mathbf{n}})_0^-,\phi_1^+ \rangle_{e_i} &\cdots& \langle (\phi_{\mathbf{n}\mathbf{n}})_0^-,\phi_{n-1}^+ \rangle_{e_i} & \langle -(\phi_{\mathbf{n}\mathbf{n}})_0^-,-\phi_0^- \rangle_{e_i} & \langle -(\phi_{\mathbf{n}\mathbf{n}})_0^-,-\phi_1^- \rangle_{e_i} &\cdots& \langle -(\phi_{\mathbf{n}\mathbf{n}})_0^-,-\phi_{n-1}^- \rangle_{e_i}\\ \langle -(\phi_{\mathbf{n}\mathbf{n}})_1^-,\phi_0^+ \rangle_{e_i} & \langle -(\phi_{\mathbf{n}\mathbf{n}})_1^-,\phi_1^+ \rangle_{e_i} &\cdots& \langle -(\phi_{\mathbf{n}\mathbf{n}})_1^-,\phi_{n-1}^+ \rangle_{e_i} & \langle -(\phi_{\mathbf{n}\mathbf{n}})_1^-,-\phi_0^- \rangle_{e_i} & \langle -(\phi_{\mathbf{n}\mathbf{n}})_1^-,-\phi_1^- \rangle_{e_i} &\cdots& \langle -(\phi_{\mathbf{n}\mathbf{n}})_1^-,-\phi_{n-1}^- \rangle_{e_i}\\ \vdots & \vdots & \vdots &\vdots &\vdots &\vdots &\vdots &\vdots\\ \langle -(\phi_{\mathbf{n}\mathbf{n}})_{n-1}^-,\phi_0^+ \rangle_{e_i} & \langle -(\phi_{\mathbf{n}\mathbf{n}})_{n-1}^-,\phi_1^+ \rangle_{e_i} &\cdots& \langle -(\phi_{\mathbf{n}\mathbf{n}})_{n-1}^-,\phi_{n-1}^+ \rangle_{e_i} & \langle -(\phi_{\mathbf{n}\mathbf{n}})_{n-1}^-,-\phi_0^- \rangle_{e_i} & \langle -(\phi_{\mathbf{n}\mathbf{n}})_{n-1}^-,-\phi_1^- \rangle_{e_i}&\cdots & \langle -(\phi_{\mathbf{n}\mathbf{n}})_{n-1}^-,-\phi_{n-1}^- \rangle_{e_i} \end{bmatrix}_{2n\times 2n}. \end{align}\]程序实现:
def edge_matrix(self,IntervalQuadrature,cfun,indx,Cdtype):
ws = IntervalQuadrature.weights
mesh = self.mesh
edge2cell = mesh.ds.edge_to_cell()
length = mesh.edge_length()
ne = mesh.edge_unit_normal()
we = self.We(IntervalQuadrature,cfun,indx,Cdtype)
jump = self.jump(IntervalQuadrature)
P = np.einsum('t, tmk, tmp, tm->mkp', ws, jump, jump,we,optimize = True)
G_Hat = self.grad_average(IntervalQuadrature,cfun,Cdtype)
S = 1/2*np.einsum('t,tmk,tmpq,mq,m->mkp',ws, jump, G_Hat, ne, length,optimize = True)
Hesse = self.Hesse_jump(IntervalQuadrature)
H = np.einsum('t, tmk, jmi ,m, tm->mki', ws, jump, Hesse , length**2 ,we,optimize = True)
ldof = self.number_of_local_dofs()
gdof = self.number_of_global_dofs()
cell2dof = self.cell_to_dof()
dof1 = cell2dof[edge2cell[:,0]]
dof2 = cell2dof[edge2cell[:,1]]
dof = np.append(dof1,dof2,axis = 1)
I = np.einsum('k, ij->ijk', np.ones(2*ldof), dof)
J = I.swapaxes(-1, -2)
# Construct the flux matrix
P = csr_matrix((P.flat, (I.flat, J.flat)), shape=(gdof, gdof))
S = csr_matrix((S.flat, (I.flat, J.flat)), shape=(gdof, gdof))
H = csr_matrix((H.flat, (I.flat, J.flat)), shape=(gdof, gdof))
return P,S,H
1.5.5. 计算右端向量
(1) 计算 $F_K = (f,v)_K$
由于在单元 $K$ 上有 $v_h = \Phi_{K^i} V_{K^i}$ , 故
\[\begin{align} (f,v_h)_{K^i} = \int_{K} f \cdot v_h\,\mathrm{dxdy} = V_{K_i}^T\int_{K} \Phi_{K^i}^T\,f\, \mathrm{dxdy} = V_{K^i}^TF_{K^i}, \end{align}\]其中
\[\begin{align*} F_{K^i} = \int_{K} \Phi_{K^i}^T\,f \mathrm{dxdy} = \begin{bmatrix} F_{0,0}^i\\ F_{1,0}^i\\ \vdots\\ F_{n-1,0}^i \end{bmatrix} = \begin{bmatrix} (f, \phi_0^i)_{K^i}\\ (f, \phi_1^i)_{K^i}\\ \vdots\\ (f, \phi_{n-1}^i)_{K^i} \end{bmatrix} = |K_i|\cdot\begin{bmatrix} \sum_{j = 0}^{t_c}w_if(P_j) \phi_0^i(P_j)\\ \sum_{j = 0}^{t_c}w_if(P_j) \phi_1^i(P_j)\\ \vdots\\ \sum_{j = 0}^{t_c}w_if(P_j) \phi_{n-1}^i(P_j) \end{bmatrix}_{n \times 1}, \end{align*}\](2) 计算 $R_{bd} = \sum_{e \in \mathcal{E}_{N}}\langle g_N,v\rangle_e$
当 $e_i \in \mathcal{E}_{D},\,e_i = \partial K^+ \cap \partial \Omega$ 时, 令
\[\begin{align*} \Phi_{K^+} = \begin{bmatrix} {\phi_0}^+ & {\phi_1}^+ & \cdots & {\phi_{n-1}}^+ \end{bmatrix}_{1\times n},\quad V_{K^+} = \begin{bmatrix} v_0^+ \\v_1^+ \\\vdots\\v_{n-1}^+ \end{bmatrix}_{n\times 1} \end{align*}\]则
\[\begin{align*} v_h|_{e_i} = \sum_{j = 0}^{n-1}{\lambda_i}^+v_i^+ = \Phi_{K^+}V_{K^+}. \end{align*}\]故
\[\begin{align*} \langle g_N,v_h\rangle_{e_i} =\int_{e_i} g_N \cdot v_h\mathrm{ds} = V_{K^+}^T\int_{e_i} \Phi_{K^+}^T\,g_N \mathrm{ds} = V_{K^+}^T(R_{bd})_{e_i}, \end{align*}\]其中
\[\begin{align*} (R_{bd})_{e_i} =\int_{e_i} \Phi_{e_i}^T\,g_N \mathrm{ds} = \begin{bmatrix} (R_{bd})_{0,0}^i\\(R_{bd})_{1,0}^i\\ \vdots \\(R_{bd})_{n-1,0}^i \end{bmatrix} = \begin{bmatrix} (g_N, \phi_0^+)_{e_i}\\(g_N, \phi_1^+)_{e_i}\\ \vdots\\(g_N, \phi_{n-1}^+)_{e_i} \end{bmatrix} = \begin{bmatrix}\sum_{j = 0}^{t_e}w_ig_N(q_j) \phi_0^+(q_j)\\ \sum_{j = 0}^{t_e}w_ig_N(q_j) \phi_1^+(q_j)\\ \vdots\\ \sum_{j = 0}^{t_e}w_ig_N(q_j) \phi_{n-1}^+(q_j)\end{bmatrix}_{n \times 1}, \end{align*}\](3) 计算 \(P_{bd} = h_e^{-1} W_e \sum_{e \in \mathcal{E}_D} \langle g_D,v\rangle_e,\,e\in \mathcal{E}_{D}\)
当 $e_i \in \mathcal{E}_{D},\,e_i = \partial K^+ \cap \partial \Omega$ 时, 有
\[\begin{align*} v_h|_{e_i} = \sum_{j = 0}^{n-1}{\lambda_i}^+v_i^+ = \Phi_{K^+}V_{K^+}. \end{align*}\]故
\[\begin{align*} h_e^{-1}W_e\langle g_D,v_h\rangle_{e_i} = h_e^{-1}W_e\int_{e_i} g_D \cdot v_h\mathrm{ds} = V_{K^+}^Th_e^{-1}W_e\int_{e_i} \Phi_{K^+}^T\,g_D \mathrm{ds} = V_{K^+}^T(P_{bd})_{e_i}, \end{align*}\]其中
\[\begin{align*} (P_{bd})_{e_i} = h_e^{-1}W_e\int_{e_i} \Phi_{e_i}^T\,g_D \mathrm{ds} = h_e^{-1}W_e\begin{bmatrix} (P_{bd})_{0,0}^i\\ (P_{bd})_{1,0}^i\\ \vdots\\ (P_{bd})_{n-1,0}^i \end{bmatrix} = h_e^{-1}W_e\begin{bmatrix} (g_D, \phi_0^+)_{e_i}\\ (g_D, \phi_1^+)_{e_i}\\ \vdots\\ (g_D, \phi_{n-1}^+)_{e_i} \end{bmatrix} = h_e^{-1}W_e\begin{bmatrix} \sum_{j = 0}^{t_e}w_ig_D(q_j) \phi_0^+(q_j)\\ \sum_{j = 0}^{t_e}w_ig_D(q_j) \phi_1^+(q_j)\\ \vdots\\ \sum_{j = 0}^{t_e}w_ig_D(q_j) \phi_{n-1}^+(q_j) \end{bmatrix}_{n \times 1}, \end{align*}\](4) 计算 $S_{bd} = \langle g_D,a\,v_\mathbf{n}\rangle_e,\,e\in \mathcal{E}_{D}$
当 \(e_i \in \mathcal{E}_D,\,e_i = \partial K_+ \cap \partial \Omega\) 时, 令
\[\begin{align*} \nabla\Phi_{K^+} = \begin{bmatrix} {\nabla\phi_0}^+ & {\nabla\phi_1}^+ &\cdots & {\nabla\phi_{n-1}}^+ \end{bmatrix}_{2\times n} \end{align*}\]则
\[\begin{align*} \nabla v_h|_{e_i} = \sum_{j = 0}^{n-1}{\nabla\phi_i}^+v_i^+ = \nabla\Phi_{K^+}V_{K^+}. \end{align*}\]故
\[\begin{align*} \langle g_D,\,a\nabla v_h\cdot \mathbf{n}\rangle_{e_i} = \int_{e_i} g_D\,a\nabla v_h\cdot \mathbf{n}\mathrm{s} = V_{K^+}^T\int_{e_i} a \nabla\Phi_{K^+}^T\cdot \mathbf{n}^T\,g_D \mathrm{ds} = V_{K^+}^T(S_{pd})_{e_i}, \end{align*}\]其中
\[\begin{align*} (S_{bd})_{e_i} = \int_{e_i} a\nabla\Phi_{K^+}^T\cdot \mathbf{n}^T\,g_D \mathrm{ds} = \begin{bmatrix} S_{0,0}^i\\ S_{1,0}^i\\ \vdots\\ S_{n-1,0}^i \end{bmatrix} = \begin{bmatrix} (g_D, a\nabla\phi_0^+\cdot \mathbf{n}^T)_{e_i}\\ (g_D, a\nabla\phi_1^+\cdot \mathbf{n}^T)_{e_i}\\ \vdots\\ (g_D, a\nabla\phi_{n-1}^+\cdot \mathbf{n}^T)_{e_i} \end{bmatrix} = \begin{bmatrix} \sum_{j = 0}^{t_e}w_ig_D(q_j) a\nabla\phi_0^+(q_j)\cdot \mathbf{n}^T\\ \sum_{j = 0}^{t_e}w_ig_D(q_j)a \nabla\phi_1^+(q_j)\cdot \mathbf{n}^T\\ \vdots\\ \sum_{j = 0}^{t_e}w_ig_D(q_j) a\nabla\phi_{n-1}^+(q_j)\cdot \mathbf{n}^T \end{bmatrix}_{n \times 1}, \end{align*}\]程序实现:
def get_right_vector(self,beta1,idx,cfun,Cdtype):
ws = self.IntervalQuadrature.weights
g0 = self.pde.dirichlet
mesh = self.mesh
space = self.space
index = mesh.ds.boundary_edge_index()
edge2cell = mesh.ds.edge_to_cell()
n = mesh.edge_unit_normal()
length = mesh.entity_measure('edge')
pp = space.bc_to_point_edge(self.IntervalQuadrature)
g_value = g0(pp)
cellidx_0 = edge2cell[:,0]
phi = space.Hat_function(pp,cellidx_0)
gphi = space.Hat_Gradients(pp,cellidx_0)
d = cfun(pp)
we = space.We(self.IntervalQuadrature,cfun,idx,Cdtype)
dgphi = np.einsum('...i, ...imn->...imn', d, gphi)
if Cdtype =='D':
bcs = np.array([1/3,1/3,1/3])
ps = space.bc_to_point_cell(bcs)
d = cfun(ps)
dgphi = np.einsum('...i, ...imn->...imn', d[cellidx_0], gphi)
P_bd = np.einsum('t, tm, tmk,tm->mk', ws, g_value[:,index], phi[:,index],we[:,index])
S_bd = np.einsum('t, tm,tmkq,mq,m->mk',ws, g_value[:,index], dgphi[:,index], n[index], length[index])
cell2dof = space.cell_to_dof()
dof1 = cell2dof[edge2cell[:,0]]
dof = dof1[index]
gdof = space.number_of_global_dofs()
P_bd = np.bincount(dof.flat, weights=P_bd.flat, minlength=gdof).reshape(-1)
S_bd = 1/2*np.bincount(dof.flat, weights=S_bd.flat, minlength=gdof).reshape(-1)
b = self.get_source_vector()
f = b + beta1*P_bd -S_bd.T
return f
2. 后验误差估计
2.1. 后验误差估计子
构造残量型后验误差估计:
\[\eta_R = \left(\sum_{K \in \mathcal{T}_h}\eta_{R,K}^2\right)^{\frac{1}{2}},\]在 $K\in\mathcal{T}_h$ 上的局部误差估计定义为
\[\eta_{R,K} = (\eta_{R_f,K}^2 +\eta_{J_\sigma,K}^2 +\eta_{J_u,K}^2 +\eta_{R_D,K}^2+ \eta_{R_N,K}^2)^{\frac{1}{2}},\]其中
\[\begin{aligned} \eta_{R_f,K}^2 &=\frac{h_K^2||f+ \nabla \cdot (a\nabla u_h)||_{0,K}^2}{a_K},\\ \eta_{R_N,K}^2 &= \sum_{e \in \mathcal{E}_K \cap \mathcal{E}_N}\frac{h_e}{a_e}||g_N - a\nabla u_h \cdot \mathbf{n}||_{0,e}^2,\\ \eta_{R_D,K}^2 &= \sum_{e \in \mathcal{E}_K \cap \mathcal{E}_D}\frac{W_e}{h_e}||g_D - u_h||_{0,e}^2,\\ \eta_{J_\sigma,K}^2 &= \frac{1}{2}\sum_{e \in \mathcal{E}_K \cap \mathcal{E}_I}\frac{h_e||[a\nabla u_h \cdot \mathbf{n]}||_{0,e}^2}{W_{e,1}},\\ \eta_{J_u,K}^2& = \sum_{e \in \mathcal{E}_K \cap \mathcal{E}_I}\frac{W_e}{h_e}||[u_h]||_{0,e}^2. \end{aligned}\]定义 $V_{DG}^{\ell}$ 空间上的能量范数:
\[||v||_{DG} := \Big(||a^{1/2}\nabla_h v||_{0,\Omega}^2 + \sum_{e \in \mathcal{E}_{ID}}h_e^{-1}W_e||[v]||_{0,e}^2\Big)^{\frac{1}{2}},\qquad v\in V_{DG}^{\ell}.\]class DDGResidualEstimators():
def __init__(self,uh,mesh,pde,p):
self.space = LagrangeFiniteElementSpace(mesh, p, spacetype='D')
self.mesh = mesh
self.qf = mesh.integrator(p+3)
self.intervalQuadrature = IntervalQuadrature(p+3)
self.pde = pde
self.p = p
self.uh = uh
self.k = self.pde.diffusion_coefficient
pass
def diffusion_coefficient(self,cfun):
p = self.mesh.barycenter()
kval = cfun(p)
return kval
def diffusion_coefficient_average(self, cfun):
edge2cell = self.mesh.ds.edge_to_cell()
lidx1 = edge2cell[:,0]
lidx2 = edge2cell[:,1]
kval = self.diffusion_coefficient(cfun)
mk = 1/2*(kval[lidx1]+kval[lidx2])
return mk
def edge_diffusion_coefficient(self,idx,cfun):
mesh = self.mesh
edge2cell = mesh.ds.edge_to_cell()
lidx1 = edge2cell[:,0]
lidx2 = edge2cell[:,1]
kval = self.diffusion_coefficient(cfun)
if idx == 1:
we = 1/2*(kval[lidx1]+kval[lidx2])
elif idx ==2:
we = (2*kval[lidx1]*kval[lidx2])/(kval[lidx1]+kval[lidx2])
elif idx ==3:
we = np.sqrt(kval[lidx1]*kval[lidx2])
return we
def uh_jump(self):
mesh = self.mesh
space = self.space
NC = mesh.number_of_cells()
cell2dof = space.dof.cell2dof
cell2edge = mesh.ds.cell_to_edge()
edge2cell = mesh.ds.edge_to_cell()
lidx1 = edge2cell[:,0]
lidx2 = edge2cell[:,1]
cell2edge2cell = edge2cell[cell2edge,0:2]
uh2cell = self.uh[cell2dof]
new_uh = uh2cell[cell2edge2cell,:].reshape(NC,3,-1)
pp = space.bc_to_point_edge(self.intervalQuadrature)
phi1 = space.Hat_function(pp,lidx1)
phi2 = space.Hat_function(pp,lidx2)
phi = np.append(phi1,-phi2,axis = 2)
new_phi = phi[:,cell2edge]
uh_jump = np.einsum('tmij,mij->tmi', new_phi,new_uh)
return uh_jump
def Rf_estimate(self,cfun):
mesh = self.mesh
space = self.space
bcs, ws = self.qf.quadpts, self.qf.weights
cell2edge = mesh.ds.cell_to_edge()
cellmeasure = mesh.entity_measure('cell')
length = mesh.edge_length(cell2edge.reshape(-1))
length = length.reshape(-1,3)
h_k = np.max(length,axis = 1)
f = self.pde.source
pp = space.bc_to_point_cell(bcs)
fval = f(pp)
fval = np.einsum('t, tm->m', ws, fval)
L_uh = space.Laplace_uh(self.uh, self.qf)
kval = self.diffusion_coefficient(cfun)
D_uh = np.einsum('t, t->t', kval, L_uh)
Rf_eta = (cellmeasure*h_k**2*(fval+D_uh)**2)/kval
return Rf_eta
def Ju_estimate(self,idx,cfun):
mesh = self.mesh
cell2edge = mesh.ds.cell_to_edge()
ws = self.intervalQuadrature.weights
index = mesh.ds.boundary_edge_index()
kval = self.edge_diffusion_coefficient(idx,cfun)
kval[index] = 0*kval[index]
we = kval[cell2edge]
uh_jump = self.uh_jump()
Ju_eta = np.einsum('t,tmi,mi->m',ws, uh_jump**2,we)
return Ju_eta
def RD_estimate(self,idx,cfun):
mesh = self.mesh
space = self.space
cell2dof = space.dof.cell2dof
cell2edge = mesh.ds.cell_to_edge()
edge2cell = mesh.ds.edge_to_cell()
index = mesh.ds.inter_edge_index()
lidx1 = edge2cell[:,0]
kval = self.edge_diffusion_coefficient(idx,cfun)
kval[index] = 0*kval[index]
we = kval[cell2edge]
ws = self.intervalQuadrature.weights
pp = space.bc_to_point_edge(self.intervalQuadrature)
phi = space.Hat_function(pp,lidx1)
phi = phi[:,cell2edge]
p = pp[:,cell2edge]
gD = self.pde.solution(p)
cell2edge2cell = edge2cell[cell2edge,0]
uh2cell = self.uh[cell2dof]
new_uh = uh2cell[cell2edge2cell]
uh_D = np.einsum('mij,tmij->tmi', new_uh,phi)
RD_estimate = np.einsum('t,tmi,mi->m', ws,(gD-uh_D)**2,we)
return RD_estimate
def Ji_estimate(self,idx,cfun):
mesh = self.mesh
space = self.space
cell2dof = space.dof.cell2dof
cell2edge = mesh.ds.cell_to_edge()
edge2cell = mesh.ds.edge_to_cell()
index = mesh.ds.boundary_edge_index()
length = mesh.edge_length()
length[index] = 0*length[index]
ne = mesh.edge_unit_normal()
length = length[cell2edge]
ws = self.intervalQuadrature.weights
lidx1 = edge2cell[:,0]
lidx2 = edge2cell[:,1]
pp = space.bc_to_point_edge(self.intervalQuadrature)
G_Hat1 = space.Hat_Gradients(pp,lidx1)
G_Hat2 = space.Hat_Gradients(pp,lidx2)
uh2cell = self.uh[cell2dof]
kval = self.diffusion_coefficient(cfun)
k3 = 1/2*(kval[lidx1]+kval[lidx2])
we = 1/k3[cell2edge]
jump1 = np.einsum('m, mj, tmjk,mk ->tm',kval[lidx1], uh2cell[lidx1] , G_Hat1,ne)
jump2 = np.einsum('m, mj, tmjk,mk ->tm',kval[lidx2], uh2cell[lidx2] , G_Hat2,ne)
jump1 = jump1[:,cell2edge]
jump2 = jump2[:,cell2edge]
Ji_estimate =1/2*np.einsum('t,tmi,mi,mi->m', ws,(jump1-jump2)**2,length**2,we)
return Ji_estimate
3. 数值案例
当精确解存在时, 记相对误差为:
\[rel-err: = \frac{||u-u_h||_{DG}}{||a^{1/2}\nabla u||_{0,\Omega}}.\] \[\begin{aligned} \eta_1 &= \left(\sum_{K \in \mathcal{T}_h}\eta_{R_f,K}^2+\eta_{J_u,K}^2 +\eta_{J_\sigma,K}^2 +\eta_{R_D,K}^2+ \eta_{R_N,K}^2\right)^{\frac{1}{2}},\\ \eta_2 &= \left(\sum_{K \in \mathcal{T}_h}\frac{h_K^2||f+ \nabla \cdot (a\nabla u_h)||_{0,K}^2}{a_K}\right)^{1/2},\\ \eta_3 &= \left(\sum_{K \in \mathcal{T}_h}\sum_{e \in \mathcal{E}_K \cap \mathcal{E}_I}\frac{W_e}{h_e}||[u_h]||_{0,e}^2\right)^{1/2}, \\ \eta_4 &= \frac{1}{2}\left(\sum_{K \in \mathcal{T}_h}\sum_{e \in \mathcal{E}_K \cap \mathcal{E}_I}\frac{h_e||[k\nabla u_h \cdot \mathbf{n]}||_{0,e}^2}{W_{e,1}}\right)^{1/2}. \end{aligned}\]间断系数问题
\[\begin{aligned} -\nabla \cdot (a(x)\nabla u) = f , \qquad & \mathbf{x} \in \Omega, \\ u = g , \qquad &\mathbf{x} \in \partial \Omega. \end{aligned}\]其中真解为
\[u(x,y) = r^{\beta}\mu(\theta),\quad r^2 = x^2 + y^2,\quad tan\,\theta = \frac{y}{x},\]$\Omega \in R^2,\Omega = [-1,1]\times [-1,1]$ 为一带 Lipschitz 边界 $\partial \Omega$ 的有界区域, 常数 $a_1 = 161.4476387975881,\, a_2 = 1$, 使得扩散系数满足 \(a(x) = \begin{cases} a_1I, &\quad xy>0\\ a_2I, &\quad xy<0 \end{cases}\)



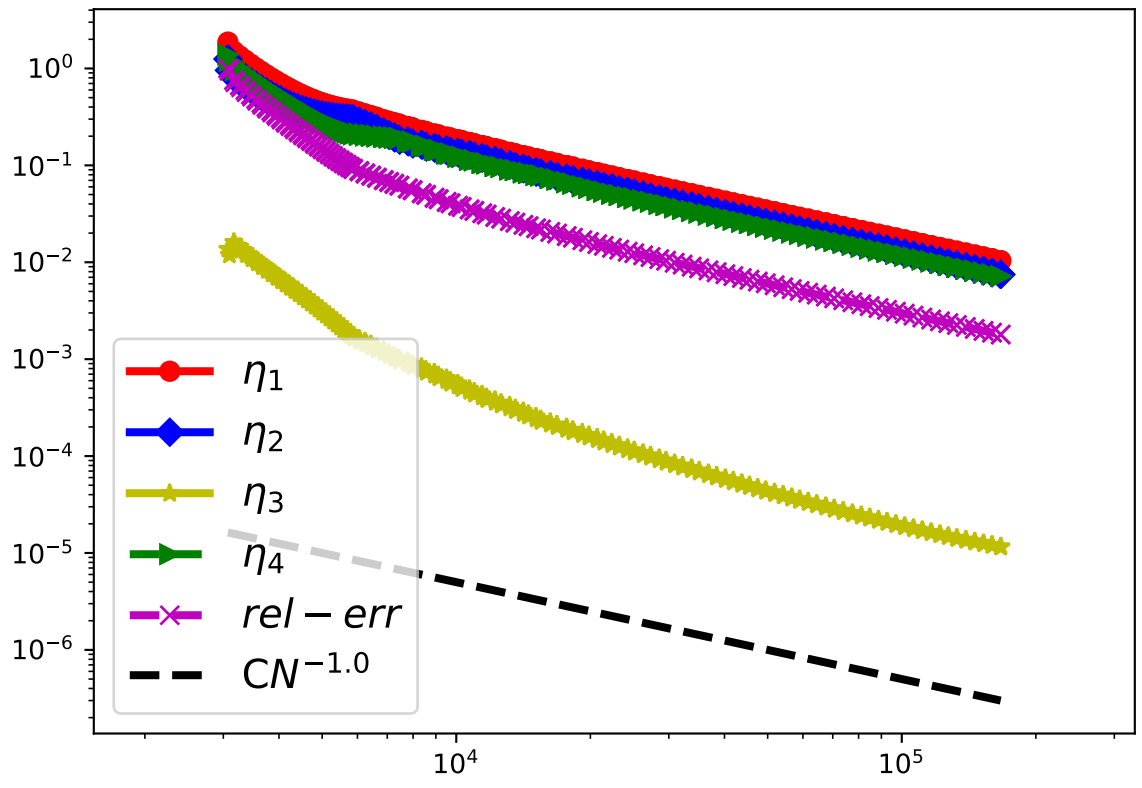
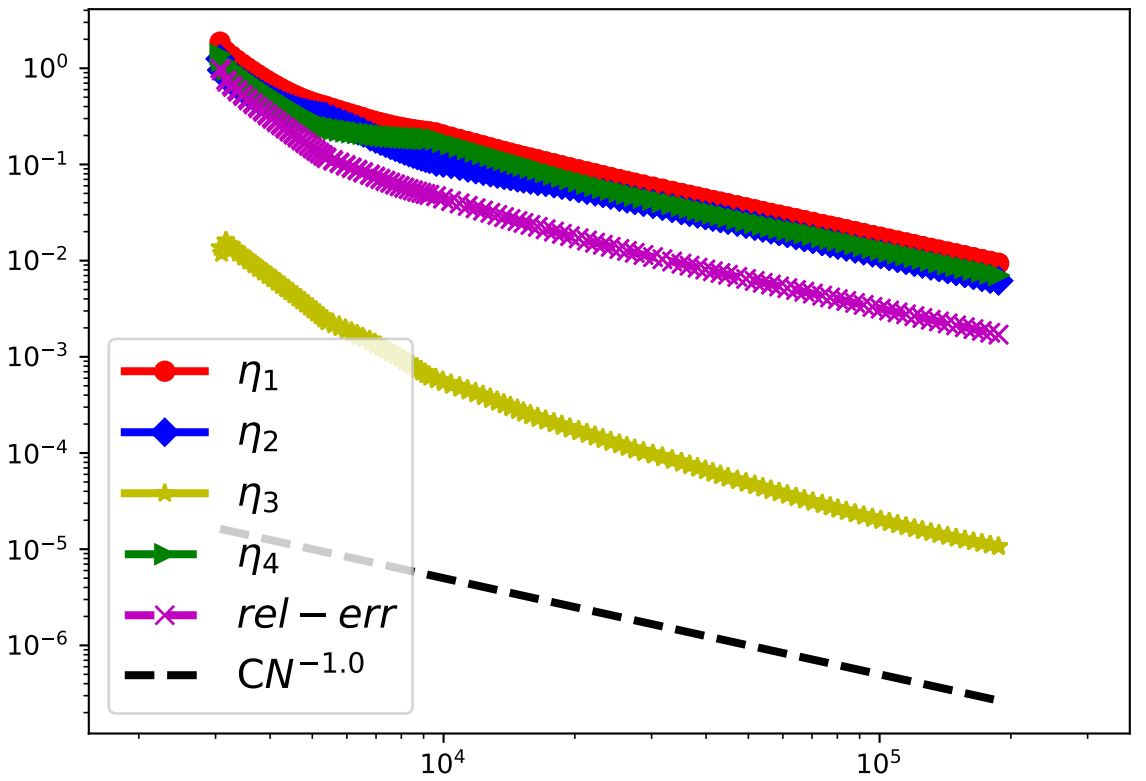

4. 参考文献
[1] H. Cao, Y. Huang, N. Yi. Adaptive direct discontinuous Galerkin method for elliptic equations. Computers and Mathematics with Applications, 97: 394-415, 2021.(https://doi.org/10.1016/j.camwa.2021.06.014)